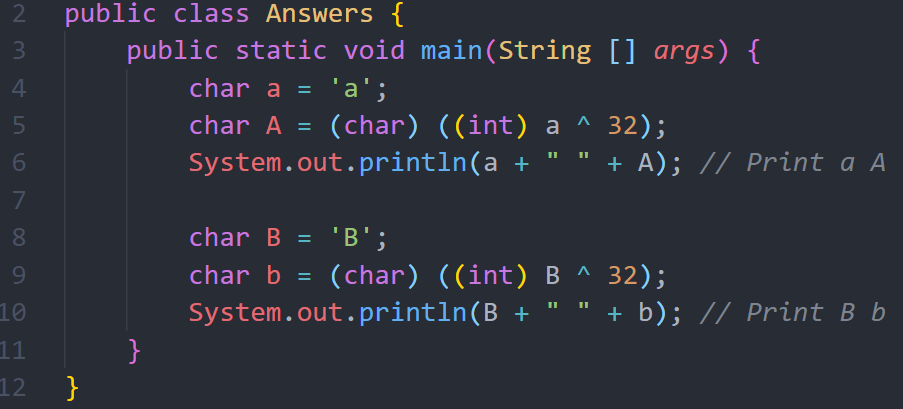
السؤال الأول:
كيف يمكن تحويل حرف من Upper Case الى Lower Case والعكس أيضاً، بدون استخدام دالة جاهزة؟
أغلب لغات البرمجة توفر مكتبات لتحويل الأحرف الصغيرة الى كبيرة أو العكس، ولكن كيف يمكن القيام بذلك بدون اللجوء للدوال الجاهزة؟
نقاط اضافية bonus: بدون استخدام علامة الجمع والطرح والجملة الشرطية if statement؟
الحل:
كل البيانات يتم حفظها في الحاسب والذاكرة على شكل مجموعة من ال Bytes (الحاسب لا يفهم الا 0/1)، ولكي نقوم بتخزين الأحرف فيجب أن تُعطى لها قيمة حتى يفهمها الحاسب وتحفظ بالشكل الثنائي Bytes.
ومن هنا وجدت أنظمة الترميز Encoding، والتي على أساسها يتم إعطاء (ترميز) أي حرف بقيمة تمثله.
من أوائل الأنظمة المستخدمة، هو نظام ترميز ASCII، ولو نظرنا للأحرف في جدول الترميز ASCII سوف نجد أنها تأخذ القيم التالية:
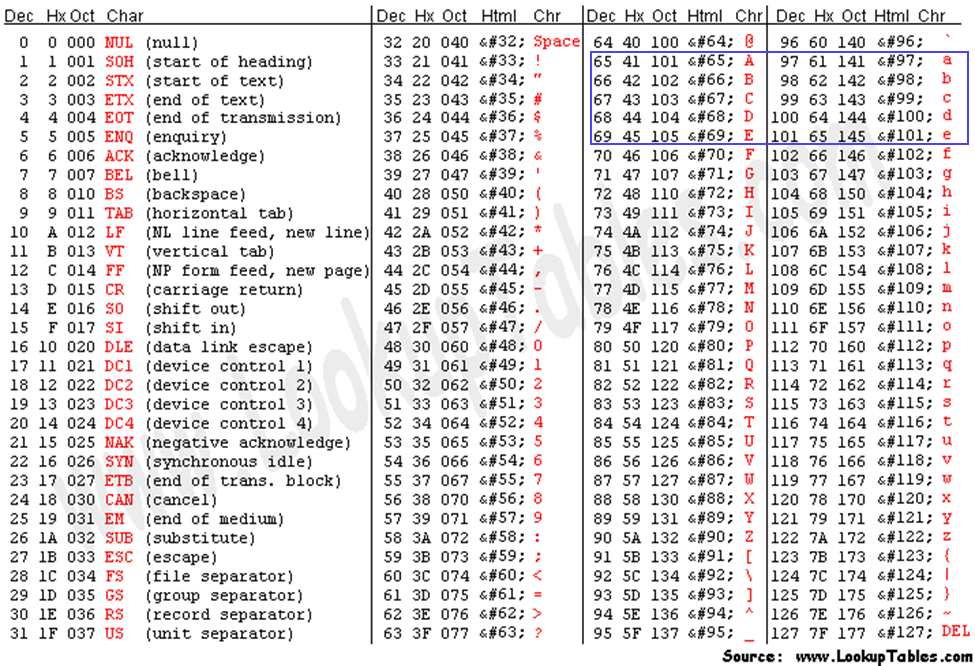
سوف تجد أن لكل حرف قيمة معينة (سواءً تم عرضها بالشكل العشري decimal أو بالشكل السداسي عشر hexadecimal أو بالشكل الثنائي binary فهي نفس القيمة ولكن بطريقة عرض مختلفة Representations).
وهذه القيمة موضحة على يسار الحرف، مثلاً الحرف A سوف تجد أنه له القيمة 65 (بالشكل العشري فهو أسهل لنا البشر)، والحرف B له القيمة 66 وهكذا. أيضاً الحرف الصغير a له القيمة 97، والحرف b له القيمة 98.
وهكذا سوف نجد أن هناك فرق ثابت هو 32 بين الأحرف الكبيرة والصغيرة.
فإذا أردنا تحويل الحرف A الى a سوف نقوم بأخذ القيمة لهذا الحرف بالشكل العشري وهي 65 ومن ثم نضيف اليها 32 وسوف تصبح a. والعكس أيضاً إذا كان لدينا الحرف b ونريد تحويله الى B فسوف نقوم بطرح 98-32 والمخرج هو 66 ونقوم بتحويلها للحرف لنحصل على B.
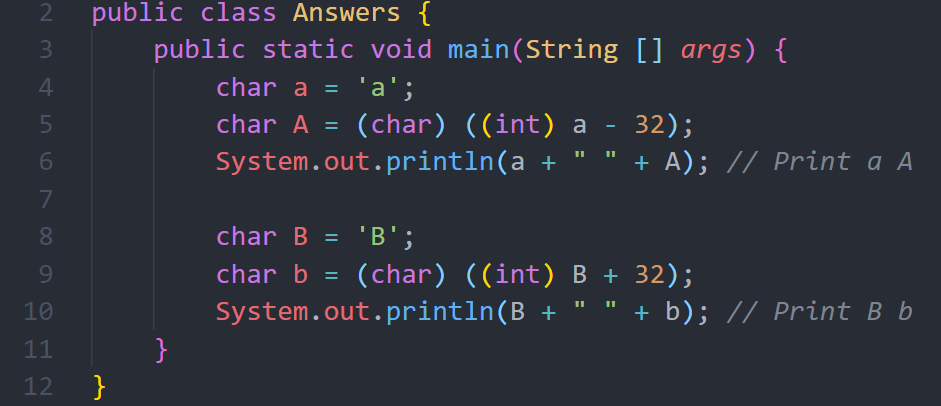
هذا الحل سوف يفي بالغرض ولكن (ليس لل Bonus J)، الحل الأفضل يعمل على مستوى bits ويقوم بعمل عكس للحرف Toggle، فاذا كان صغيراً فسيتم التحويل الى حرف كبير والعكس أيضاً وبدون استخدام عمليات جمع وطرح أو حتى جمل شرطية، الصورة التالية توضح الحل:
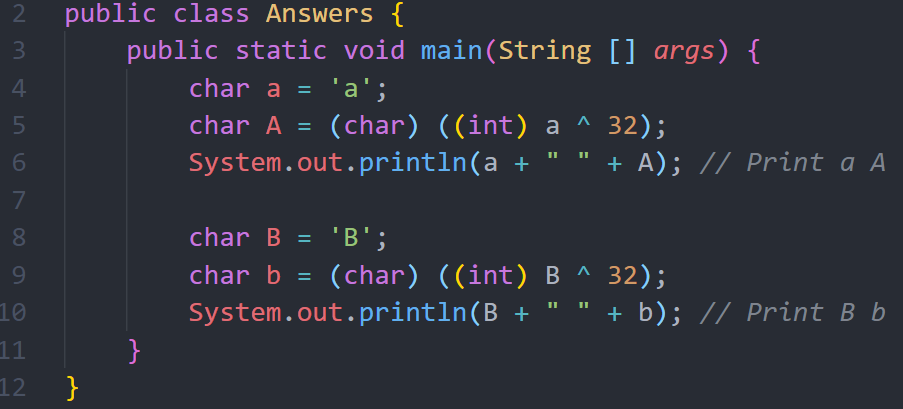
بالتأكيد تراودك الكثير من الأسئلة، وما هو هذا الرقم 32 وما هي العملية ^ ولماذا، وسوف نجيب على هذه الأسئلة بالتفصيل، ونبدأ بعمل مراجعة بسيطة لل bits/bytes ومرحباً بك في عالم ال Bitwise.
مراجعة: ال Bytes/Bits والعمليات عليها
الحواسيب تتعامل مع ال bits/bytes فقط، والبايت يتكون من 8 بت bits، البت الأول من جهة اليمين يسمى ال Least Significant Bit واختصاراً LSB، والبت الأخير (أو الأول من اليسار) هو ال Most Significant Bit واختصاراً MSB.
أقل قيمة للبايت هو 00000000 وهي 0 بالشكل العشري، وأعلى قيمة هي 11111111 وهي 255 بالشكل العشري، الشكل التالي يعرض 00101101 وهي لها القيمة العشرية 45، تستطيع معرفتها عن طريق جمع قيمة الخانات التي بها 1 وسوف تجد أن القيمة هي 45.
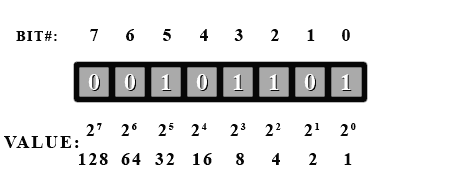
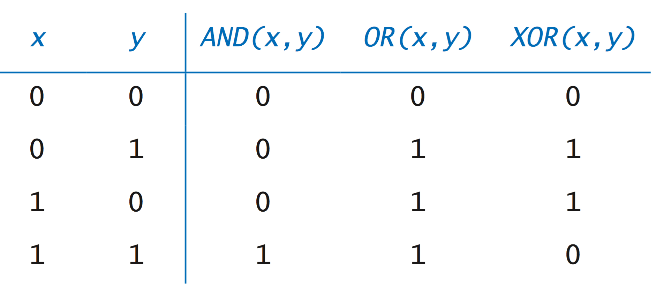
هناك العديد من العمليات Bitwise Operation التي يمكن أن تتم على ال bits وهي AND, OR, XOR، الصورة التالية توضيح نتيجة العمليات بهما:
الصورة التالية تبين مثال على استخدام كل من AND, OR, XOR كما يلي:

حل الأمثلة بهذه العمليات عملية بسيطة لكل من درس الدوائر المنطقية أو الجبر المنطقي، ولكن من المهم استنباط بعض المفاهيم والتي سوف تسهل بعض العمليات التالية وهي:
- في ال OR:
- أي مدخل OR 1 = 1
- أي مدخل OR 0 = المدخل نفسه
- في ال AND:
- أي مدخل AND 1 = المدخل نفسه
- أي مدخل AND 0 = 0
- في ال XOR:
- أي مدخل XOR 0 = المدخل نفسه (إذا كأن أحد المدخلات 1 فقط، النتيجة 1)
- إذا المدخلين متشابهين = 0
في كثير من الأحيان يكون لدينا بايت، ونريد عمل عملية معينة عليها، مثلاً تحويل بت معينة الى 0 أو 1 وهكذا، فسوف نحتاج الى استخدام أحد العمليات AND,OR,XOR ووضع مدخل ثاني نقوم بكتابته بطريقة ما بحيث نحصل على المخرج المطلوب هذ العملية تدعى Masking.
هناك عدة عمليات عديدة مشهورة في ال Masking:
- وضع 1 على بت معينة في البايت Setting Bit
- تصفير (أي وضع 0) على بت معينة في البايت Clear Bit
- عكس حالة بت معينة في البايت Toggle Bit
- الحصول على Bit معينة من البايت Getting a Bit
فيما يلي سوف نوضح هذه العمليات، لأنها تعد من أشهر التطبيقات على ال bitwise.
وضع بت معينة Setting Bit
سوف نعمل على العدد 73 وهو 0100 1001 بالشكل الثنائي، وليكن نريد وضع 1 على البت الثالثة بحيث يكون الناتج هو 0100 1101 وهو يساوي 77، فما هي العملية اللازمة بالإضافة الى المدخل الثاني الذي من خلالها أستطيع الحصول على ذلك المخرج؟

لو تذكرنا مفاهيم ال OR وهي: أي مدخل OR 1 = 1، وأي مدخل OR 0 = المدخل نفسه، سوف نستطيع اكمال الفراغات بسهولة، فطالما نريد المخرج كما هو سوف تكون كل الخانات 0، ما عدا الخانة التي نريد وضعها ب 1 سوف تكون 1، الشكل التالي يبين النتيجة:

اذاً لعمل Settings للبت في أي مدخل دائماً نستخدم OR، ونحدد 1 في الخانة التي نريد تحديدها والبقية 0.
فيما يلي مثال لعمل Setting ل bit معينة، وذلك عن طريق ال ORing with 1 في الخانة التي نريد وضعها وبقية الخانات تكون صفر، وبالتالي نحافظ عليها كما هي. المثال يعرض طريقة ال ORing بعدة طرق مختلفة وهي جميعاً نفس النتيجة.
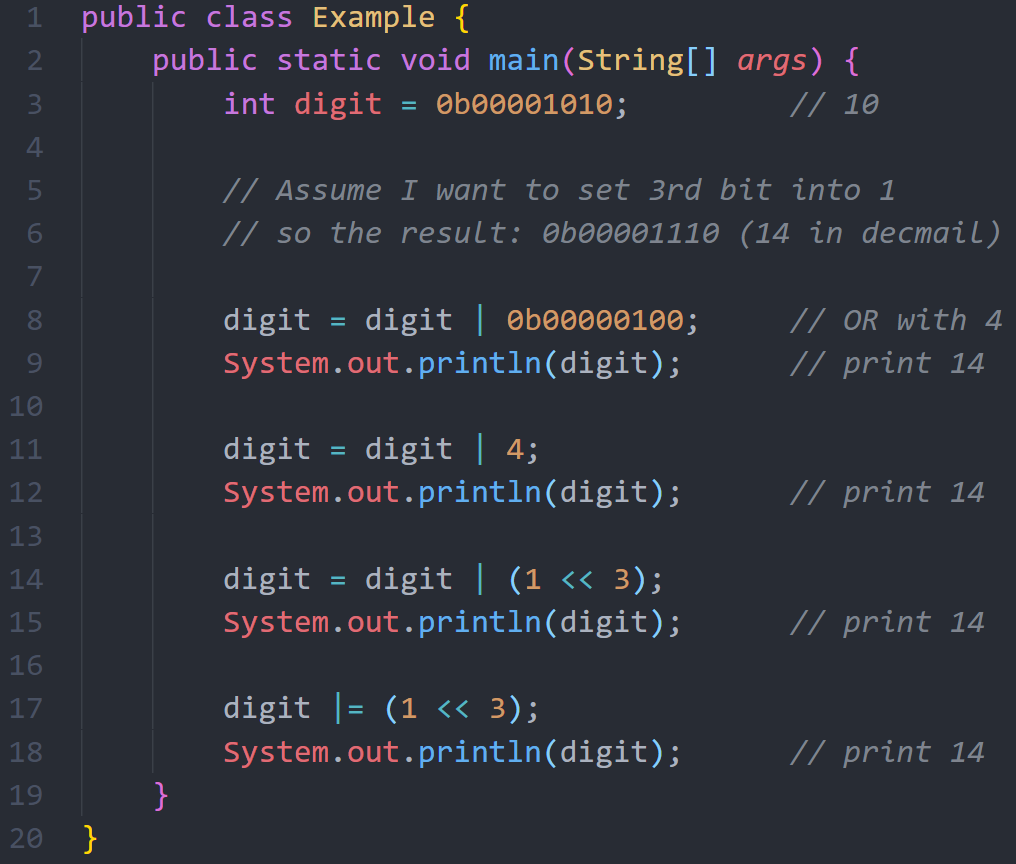
هناك أمور يجب ملاحظتها:
- السطر 3: قمنا بكتابة العدد 10 بالشكل الثنائي، وهذا طبيعي حيث تسمح أغلب لغات البرمجة بال Literal binary or hex.
- السطر الثامن: قمنا بعمل XOR العدد 10 مع المدخل الثاني وقمنا بكتابتها كاملاً بالشكل الثانئي
- السطر 11 قمنا بكتابة المدخل الثاني بالشكل العشري (XOR لا تهتم بتمثيله بأي نظام كان)
- السطر 14: قمنا بعملية مثيرة هنا، وهي الازاحة Shift حيث تم الازاحة الى اليسار 3 خطوات وبالتالي نحصل على نفس النتيجة وهي العدد 4 او بالشكل الثنائي له.
- السطر 17: ايضاً طريقة مختصرة لكتابة العملية وهي معروفة a = a + 1 يمكن اختصارها الى a += 1.
لماذا استخدمنا الازاحة Shift؟
برمجياً بدلاً من أن يتم كتابة ال Mask بهذا الطريقة 00000100 فهي قد تكون متعبة، ليكن نريد عملها على البت الرابع أو الثالث فكل ما نحتاج أن نكتب البايت كاملاً. لذلك يمكن أن نستخدم عملية الازاحة Shift، ونقول نبدأ بالعدد 1 (والذي هو 0000 0001) ومن ثم نقول نريد إزاحة لليسار بمقدار 5 وهي العملية 1 << 5 وسوف نحصل على 0010 0000 وبعدها نقوم بتطبيق عملية XOR. وبالتالي سوف يصبح شكلها هو: Byte XOR (1 << 5)
تصفير بت معينة Clear Bit
سوف نعمل على العدد 73 وهو 0100 1001 بالشكل الثنائي، وليكن نريد تصفير البت الرابعة بحيث يكون الناتج هو 0100 0001 وهو يساوي 65، فما هي العملية اللازمة بالإضافة الى المدخل الثاني الذي من خلالها أستطيع الحصول على ذلك المخرج؟

لو تذكرنا مفاهيم ال AND وهي: أي مدخل AND 1 = المدخل نفسه، وأي مدخل AND 0 = 0، سوف نستطيع اكمال الفراغات بسهولة، فطالما نريد المخرج كما هو سوف تكون كل الخانات 1، ما عدا الخانة التي نريد تصفيرها سوف تكون 1، الشكل التالي يبين النتيجة:

اذاً لعمل Clear للبت في أي مدخل دائماً نستخدم AND، ونحدد 1 في الخانات التي نريدها كما هي، و0 للخانة المراد تصفيرها.
فيما يلي مثال لعمل Clear ل bit معينة، وسوف نستخدم AND هنا ونضع 1 في كل الخانات لكي نحافظ عليها، ما عدا الخانة التي نريدها وتكون 0. المثال التالي يستعرض هذه الفكرة:
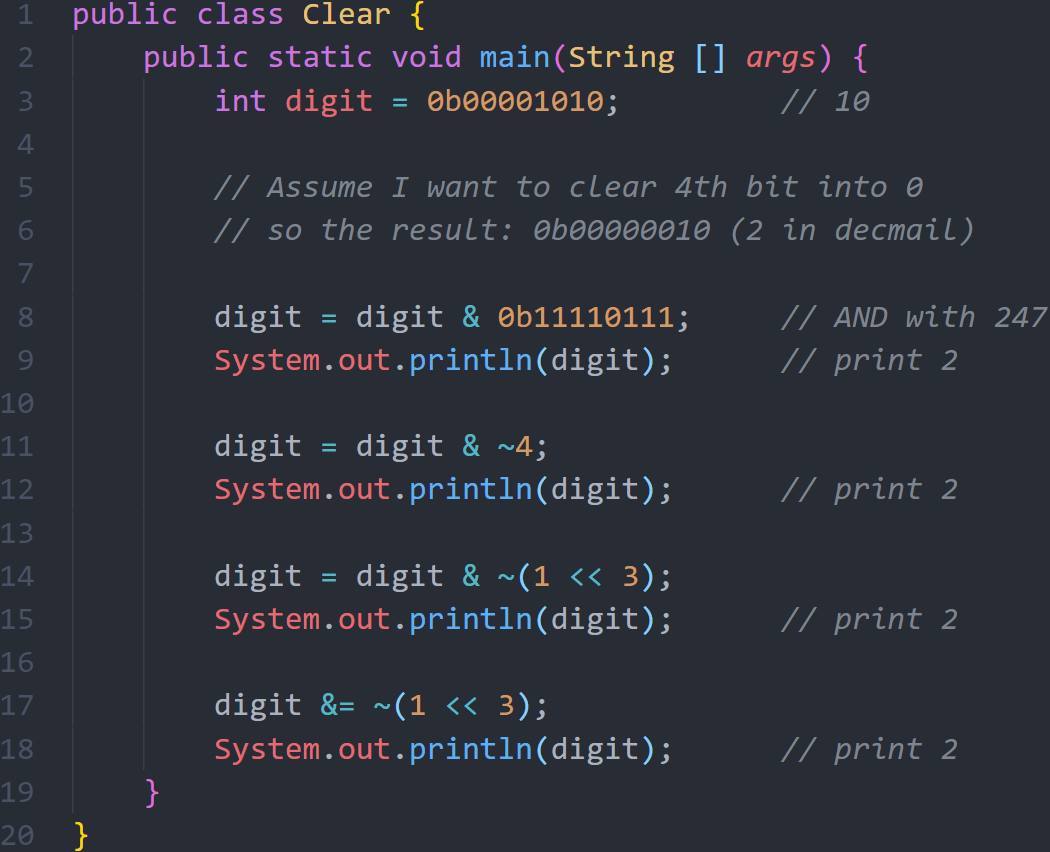
لاحظ التالي:
- السطر 8: قمنا بكتابة البايت كاملاً بالطريقة الثنائية
- السطر 11: وهذه عملية مثيرة ايضاً، وهي المتمم، والمتمم هو عكس كل البتات (اذا كانت صفر تكون 1 والعكس)، فالان بدلاً من كتابة كل ال bytes 1 والخانة التي اريدها 0، سوف أحد الخانة التي اريدها ب 1 والبقية صفر والعدد الناتج هو أربعة، ومن ثم نحسب المتمم له ونحصل على نفس المدخل في السطر 8.
- السطر 14: وهنا استخدمنا الازاحة حتى نحصل على الأربعة، ومن ثم المتمم لنحصل على الرقم 247 بالشكل الثنائي.
- السطر 15: وهي نفس العملية بشكل مختصر، وسبق تناولها في المثال السابق.
عكس بت معينة Toggle Bit
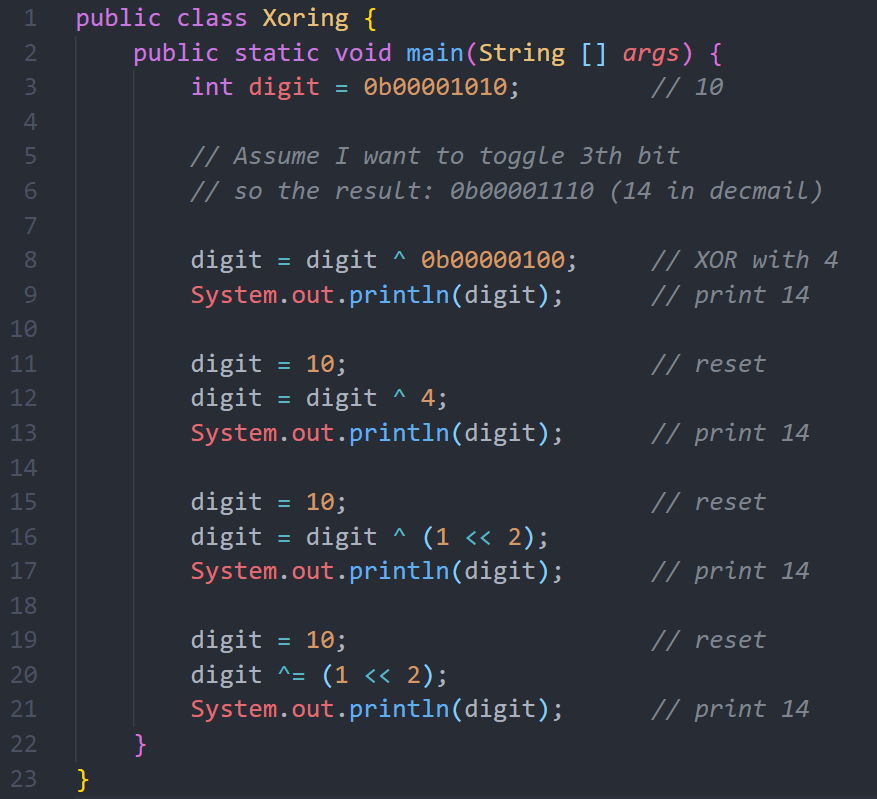
سوف نعمل على العدد 73 وهو 0100 1001 بالشكل الثنائي، وليكن نريد عكس قيمة البت الثانية (إذا كانت واحد تصبح 0، والعكس إذا كانت 0 تصبح 1) بحيث يكون الناتج هو 0100 1011 وهو يساوي 75، فما هي العملية اللازمة بالإضافة الى المدخل الثاني الذي من خلالها أستطيع الحصول على ذلك المخرج؟

لو تذكرنا مفاهيم ال XOR وهي: إذا كان أحد المدخلات 1 فقط، النتيجة 1، وإذا كان المدخلين متشابهين فالنتيجة 0، سوف نستطيع اكمال الفراغات بسهولة، فطالما نريد المخرج كما هو سوف تكون كل الخانات 0، ما عدا الخانة التي نريد وضعها عكسها سوف تكون 1، الشكل التالي يبين النتيجة:

اذاً لعمل Toggle للبت في أي مدخل دائماً نستخدم XOR، ونحدد 1 في الخانة التي نريد عكسها والبقية 0. مثال:
جلب بت معينة Checking Bit
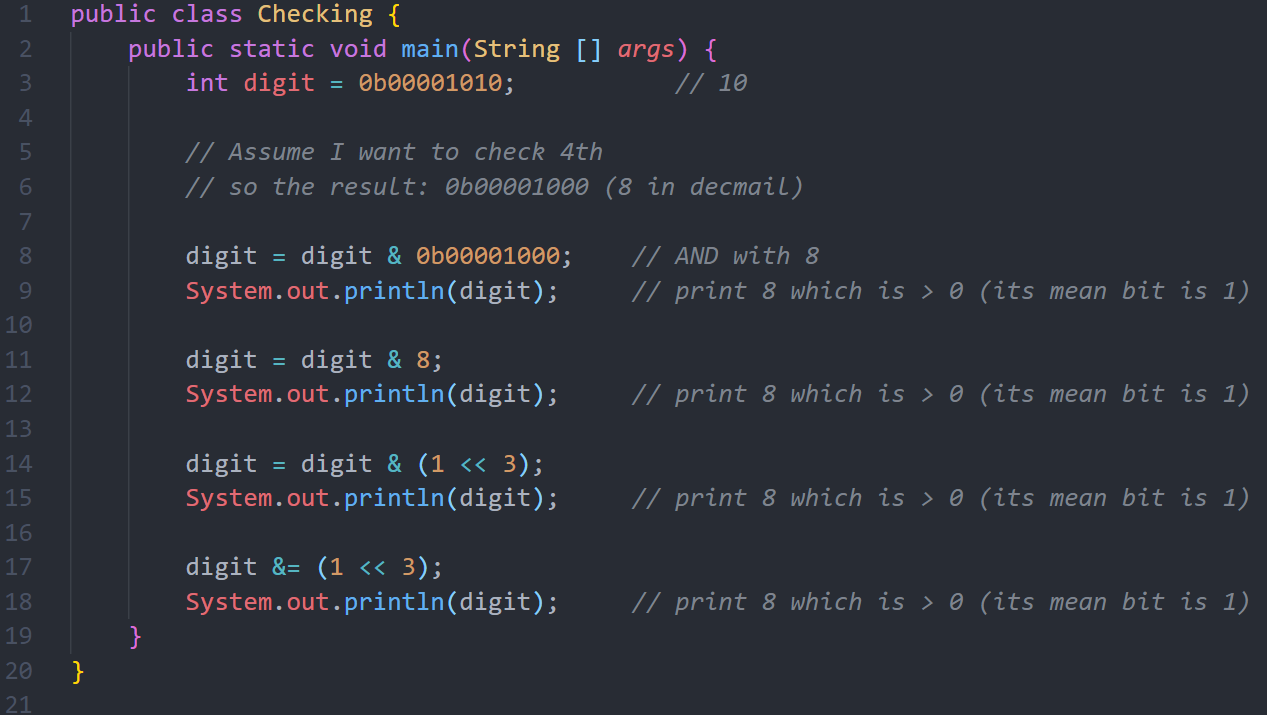
سوف نعمل على العدد 73 وهو 0100 1001 بالشكل الثنائي، وليكن نريد معرفة البت السابع وهو 1، فما هي العملية اللازمة بالإضافة الى المدخل الثاني الذي من خلالها أستطيع الحصول على ذلك المخرج؟

لو تذكرنا مفاهيم ال AND وهي: أي مدخل AND 1 = المدخل نفسه، وأي مدخل AND 0 = 0، سوف نستطيع اكمال الفراغات بسهولة، فطالما غير مهتمين بالخانات فسوف نضع 0 عليها حتى تخرج 0، وفقط 1 في المكان الذي نريده، الشكل التالي يبين النتيجة:

اذاً لعمل Check للبت في أي مدخل دائماً نستخدم AND، ونحدد 1 في الخانات التي نريدها كما هي، و0 للخانة المراد تصفيرها، وبعد ذلك نفحص النتيجة إذا كانت 0 فهي يعني أن البت كان 0، والا بغض النظر عن القيمة سوف نعرف أنه 1.
المثال التالي يعرض ال Checking، وسوف نلاحظ أنه بعد عمل ANDing مع ال 1 في الخانة المطلوبة فحصها والبقية 0، أن المخرج اما أن يكون 0 (في حال الخانة 0) أو أي قيمة أخرى في حال كانت 1.
الان نعودنا نرجع للسؤال
وهو كيف نحول من حرف صغير الى كبير أو العكس بدون استخدام عمليات الجمع والطرح، وسوف نحتاج أن ننظر الى جدول الأسكي مجدداً، ولكن هذه المرة سنتعرض ال Binary Representation (في الجدول السابق الخاص بالاسكي عرضنا التمثيل Decimal, Hex, Oct ولكن الجدول بالأسفل يعرضها بالشكل الثنائي):

سوف نلاحظ شيئاً مهماً في الجدول أعلاه، وهو أن للحروف نفس القيمة في التمثيل الثنائي، ما عدا البت السادس (من اليمين)، هذا البت في حالة كان به قيمة سوف يزيد القيمة ب 32، ولذلك سوف نجد أنه 0 في الأحرف الكبيرة، ومتواجد 1 في الأحرف الصغيرة.
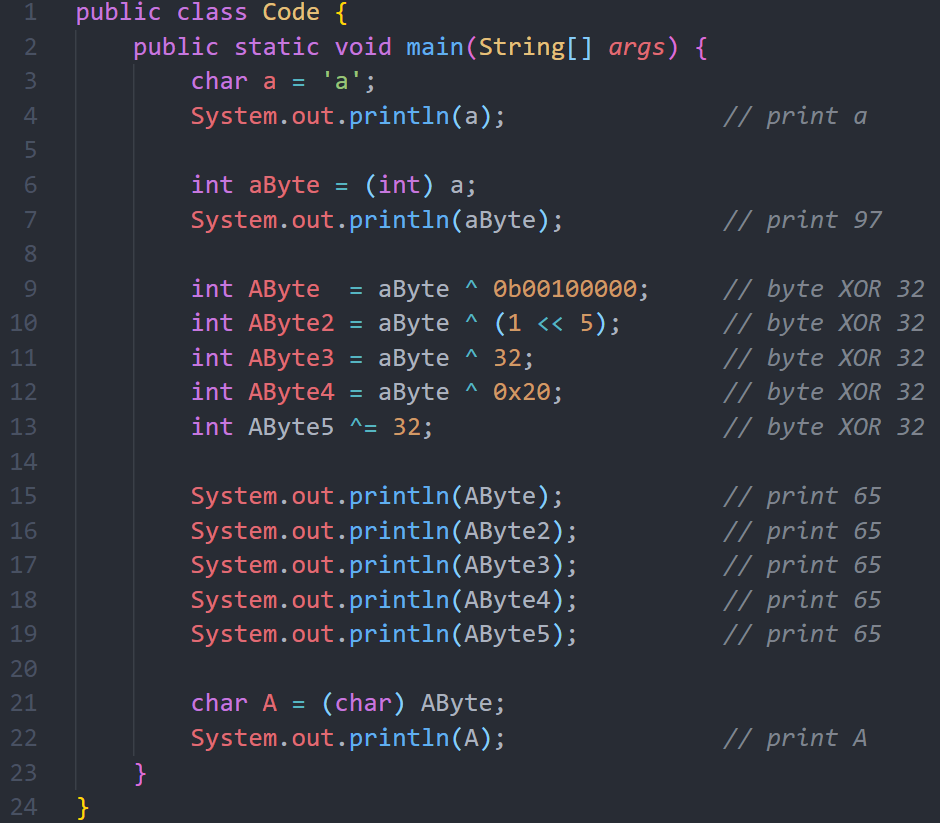
اذاً المطلوب هو تغيير قيمة هذه البت، وسوف نستخدم ال XOR، ونقوم بعملية XOR بين قيمة الحرف مع القيمة 32 (أو 20Hex)، وهذه القيمة سوف تدع كل البتات bits كما هي، فقط البت السادس سوف يتم عكسه، إذا كان واحد سوف يصبح 0، وإذا كان 1 سوف يصبح 0. الصورة التالية توضح النتيجة:

في مثالنا أعلاه قمنا بعمل Toggle للبت السادس عن طريقة XOR القيمة مع 32 وهو 0010 0000 بالشكل الثنائي.
وهذا هو الحل برمجياً:
ال Bitwise لا تنتهي تطبيقاته هنا، وهي تستخدم في التشفير، الضغط، وحتى في تحديد الخيارات مثلاً فتح ملف للقراءة والاضافة، وايضاً في طريقة تحديد الصلاحيات، وسوف نتناول بعضاً من هذه الطرق للمزيد في المستقبل في مقالات ودروس حولها.
الى هنا وصلنا لنهاية حل السؤال، أرجوا أن تكونوا قد استفدتم من الحل.
تمارين:
- كيف يمكن معرف هل العدد زوجياً أم فردياً؟ بدون استخدام معامل باقي القسمة (عن طريق ال bitwise)
- قم بعمل Swap بين متغيرين بدون استخدام متغير ثالث؟ (استخدم XOR)
مراجع للاستزادة:
- أساسيات لا بد لأي مبرمج معرفتها الترميز (Encoding):
- How do you set, clear, and toggle a single bit?
- مقدمة حول معاملات ال Bit لجميع المبرمجين
- مقدمة حول معاملات ال Bit لجميع المبرمجين 2
- Mask (computing)
تجمع المطورين السودانيين
24-08-2020
sudandev.org